Unit Circle & Tangent: Learn, Graph, And Solve Trigonometry
Can a simple circle unlock the secrets of trigonometry, helping you navigate angles and functions with ease? The unit circle, a seemingly straightforward geometric construct, is the key to unlocking a deeper understanding of trigonometric functions and their applications.
The unit circle, a circle with a radius of precisely 1, sits at the heart of trigonometry. Its elegance lies in its ability to provide a visual and intuitive framework for understanding and calculating trigonometric functions. Unlike the abstract definitions often found in textbooks, the unit circle offers a tangible way to grasp concepts like sine, cosine, and tangent.
Let's delve into the fundamental aspects of how the unit circle functions as a tool for understanding and calculating trigonometric functions, and related information.
| Feature | Details |
|---|---|
| Definition of Unit Circle | A circle with a radius of 1 unit, centered at the origin (0,0) of a Cartesian coordinate plane. |
| Key Components |
|
| Trigonometric Functions Explained |
|
| Applications |
|
| Pythagorean Theorem |
|
For more in-depth information, you can consult authoritative resources such as Math is Fun - The Unit Circle.
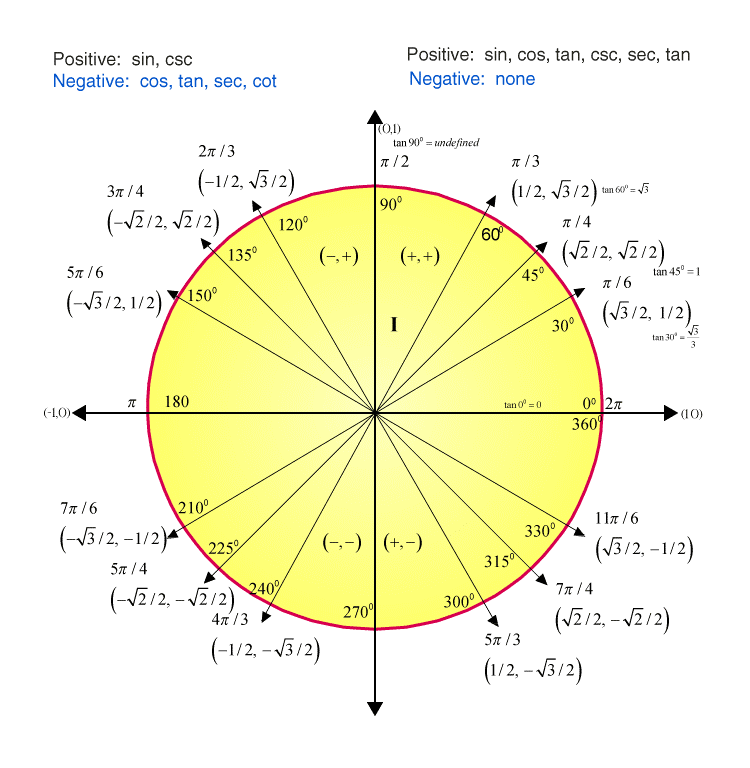
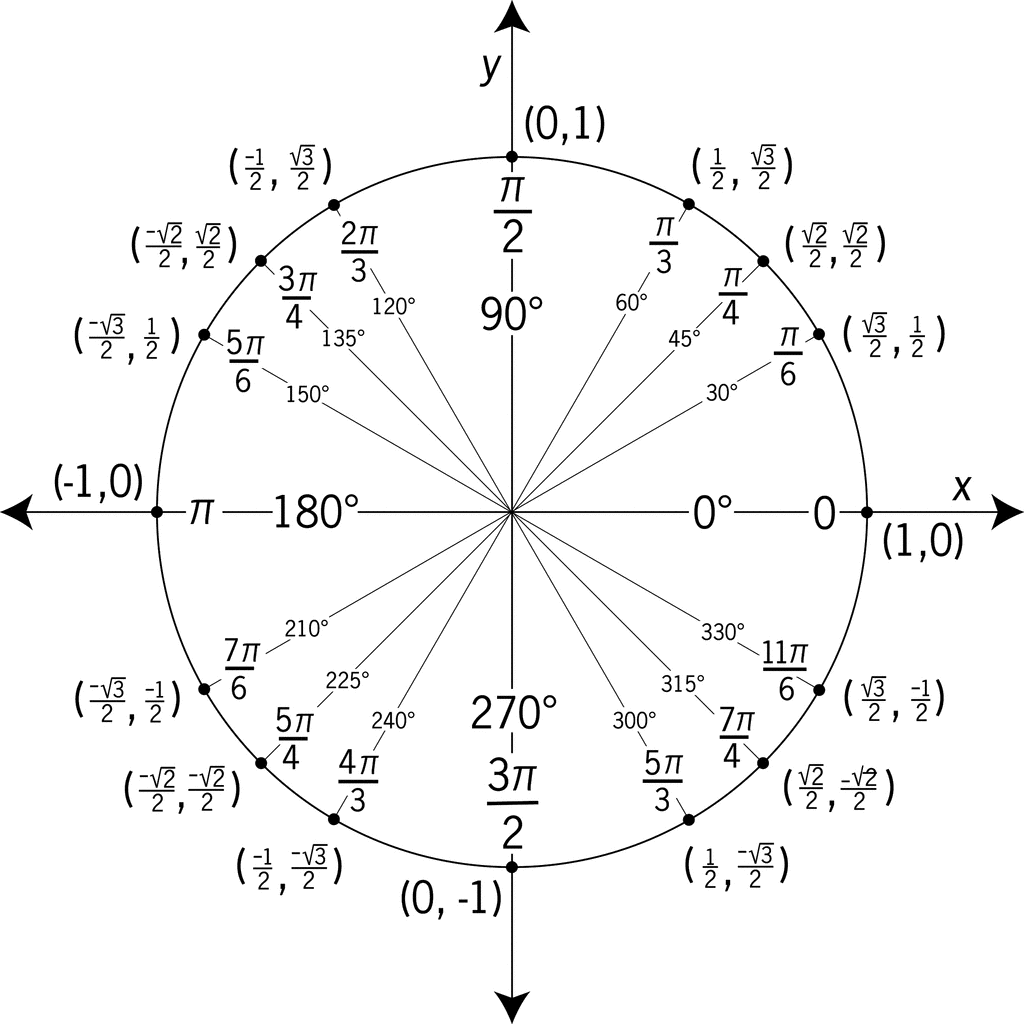
The unit circle is more than just a geometric shape; its a dynamic tool that allows us to explore and visualize the behavior of trigonometric functions. The angles, measured in either degrees or radians, sweep around the circle, and for each angle, we can determine the corresponding values of sine, cosine, and tangent.
Consider a point P on the circumference of the unit circle. The coordinates of P are represented as (x, y). Here's how the core functions are defined:
- Sine (sin ): The y-coordinate of P. It represents the vertical distance from the point P to the x-axis.
- Cosine (cos ): The x-coordinate of P. It represents the horizontal distance from P to the y-axis.
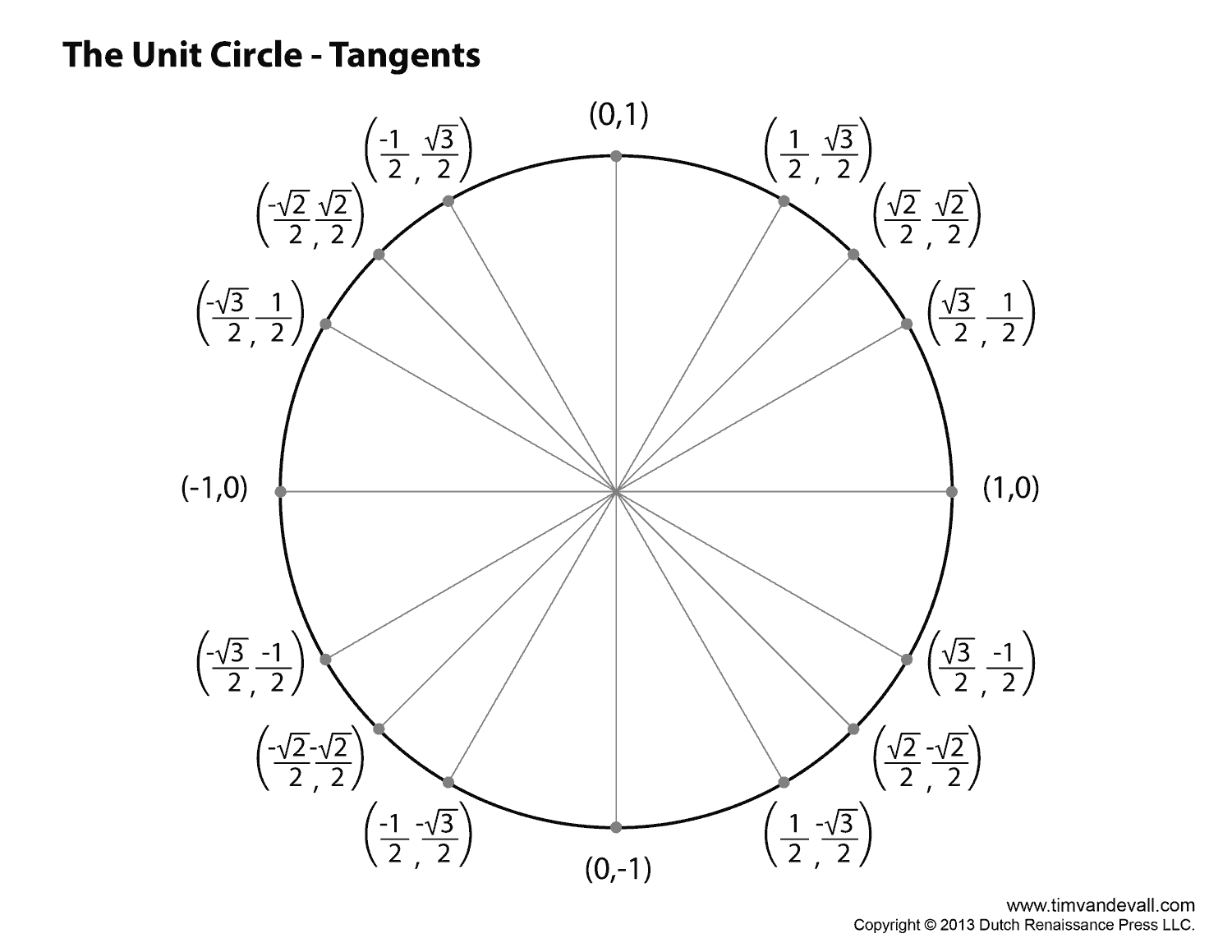
- Tangent (tan ): Defined as the ratio of sine to cosine (sin / cos ). Geometrically, it's the slope of the line segment from the origin to point P. It also corresponds to the length of a tangent line segment drawn from the point on the circle to the x-axis.
One of the major advantages of using the unit circle is its ability to extend the definition of trigonometric functions beyond the confines of acute angles (0 to 90 degrees). As the angle rotates around the circle, the sine, cosine, and tangent values change in predictable ways.
For angles greater than 90 degrees, the unit circle provides an intuitive way to understand their trigonometric values. For instance:
- In the second quadrant (90 < < 180), sine is positive (y-coordinate is positive), and cosine is negative (x-coordinate is negative).
- In the third quadrant (180 < < 270), both sine and cosine are negative.
- In the fourth quadrant (270 < < 360), sine is negative, and cosine is positive.
The relationship between the unit circle and the tangent function is a crucial one. While sine and cosine are directly represented by the coordinates on the circle, the tangent is calculated using these coordinates. Specifically, tan = sin / cos . This relationship has a significant implication: tangent is undefined when cos = 0. This happens at 90 and 270 (and their coterminal angles), where the x-coordinate (cosine) of the point on the unit circle is zero. The unit circle elegantly illustrates this and helps avoid the conceptual hurdle of trying to define tangent based solely on opposite and adjacent sides in a right triangle.
To calculate the values of sine, cosine, and tangent for any angle, you need to know the coordinates of the point where the terminal side of the angle intersects the unit circle. Here's how it works:
- Standard Position: An angle is drawn in standard position with its vertex at the origin (0, 0) of the coordinate plane and its initial side along the positive x-axis.
- Terminal Side: The terminal side of the angle is the ray that rotates from the initial side.
- Intersection: The point where the terminal side intersects the unit circle determines the values of the trigonometric functions. The x-coordinate of this point is the cosine of the angle, and the y-coordinate is the sine of the angle. The tangent is then calculated using the ratio sin / cos .
Using the unit circle and understanding the concept of reference angles, which is the acute angle formed between the terminal side of an angle and the x-axis, allows you to determine the values of sine, cosine, and tangent for any angle by relating them to the values of angles in the first quadrant (0 to 90). The signs of the functions depend on the quadrant in which the terminal side of the angle lies.
Let's consider some example angles and their corresponding trigonometric values using the unit circle.
| Angle (Degrees) | Angle (Radians) | sin() | cos() | tan() | Quadrant |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | On x-axis |
| 30 | /6 | 1/2 | 3/2 | 3/3 | I |
| 45 | /4 | 2/2 | 2/2 | 1 | I |
| 60 | /3 | 3/2 | 1/2 | 3 | I |
| 90 | /2 | 1 | 0 | Undefined | On y-axis |
| 120 | 2/3 | 3/2 | -1/2 | -3 | II |
| 135 | 3/4 | 2/2 | -2/2 | -1 | II |
| 150 | 5/6 | 1/2 | -3/2 | -3/3 | II |
| 180 | 0 | -1 | 0 | On x-axis | |
| 210 | 7/6 | -1/2 | -3/2 | 3/3 | III |
| 225 | 5/4 | -2/2 | -2/2 | 1 | III |
| 240 | 4/3 | -3/2 | -1/2 | 3 | III |
| 270 | 3/2 | -1 | 0 | Undefined | On y-axis |
| 300 | 5/3 | -3/2 | 1/2 | -3 | IV |
| 315 | 7/4 | -2/2 | 2/2 | -1 | IV |
| 330 | 11/6 | -1/2 | 3/2 | -3/3 | IV |
| 360 | 2 | 0 | 1 | 0 | On x-axis |
Understanding the unit circle provides a clear, consistent method to determining these trigonometric function values.
Furthermore, the unit circle aids in visualizing and understanding the concept of the periodic nature of trigonometric functions. As the angle continues to rotate around the circle, the sine, cosine, and tangent values repeat. Sine and cosine have a period of 2 (or 360), meaning their values repeat every 2 radians or 360 degrees. Tangent has a period of (or 180), which signifies that its values repeat every radians or 180 degrees.
Consider the graph of y = tan(x). The unit circle helps determine key features for the graph:
- Asymptotes: Tangent is undefined at x = /2, 3/2, and so forth, leading to vertical asymptotes at these points.
- Zeros: The tangent is zero at x = 0, , 2, and so on.
- Periodicity: The graph repeats itself every units.
To graph y = tan(x) + 1, you simply shift the tan(x) graph one unit upward. The asymptotes remain the same, but the zeros are now at x = 0, , 2, and so on. the output values is increased by 1.
In summary, the unit circle is an invaluable tool for understanding and applying trigonometry. It facilitates calculations, provides visual clarity, and enhances the ability to grasp the concepts of angles, functions, and periodic behavior. It serves as a strong foundation for more advanced trigonometric studies. The unit circle is a gateway to a deeper appreciation of the elegant relationships between angles, coordinates, and the fundamental trigonometric functions.
By grasping the unit circle, students and enthusiasts alike can move beyond simple memorization and develop a true understanding of the trigonometric functions and their uses.